martes, 22 de noviembre de 2016
jueves, 17 de noviembre de 2016
PROBLEMAS ECUACIÓN DE LA RECTA: URL
https://docs.google.com/document/d/1j6VVCmKC-rXG4YRlarjEvyQ8nh565_GiIxS-8mG6-Ww/edit?usp=sharing
martes, 25 de octubre de 2016
AMOR DE TEOREMA (Calavera literaria)
AMOR DE TEOREMA.
Estaba una chinita
de ojitos colorados,
se dice llamar catrina,
porque asusta en todos lados.
Andaba buscando
aun filósofo y matemático
de barba larga y cabello claro.
Pitágoras se llama,
aquel muchacho guapo,
que le encanta la comida,
pero también el canto.
Estaba Pitágoras un teorema inventando,
cuando llego la catrina
y lo saco del cuarto.
Te propongo un trato,
dijo asustado;
la catrina pensando
y el casi llorando.
Te enseño mi teorema,
pero no me hagas daño,
la catrina tomó un banco,
y estuvo escuchando.
Pon mucha atención,
es muy fácil de aprender,
y si lo comprendes
unos tacos te invito a comer.
En todo triángulo rectángulo,
el cuadrado de la longitud de la hipotenusa
es igual a la suma de los cuadrados
de sus catetos.
Para que lo puedas comprender,
un ejemplo de te voy a poner,
pero escucha muy bien,
que solo repito una vez.
En el triangulo rectángulo
esta el Sr. Archus (a) y la Sra. Bithais (b)
ellos dos se quieren,no lo pueden negar,
se dan mucho amor y sin pensar
una hipotenusa van a crear,
que por nombre va a llevar Claps (c).
Entonces se formula que:
claps=√(〖archus〗^2 )+〖bithais〗^2
pero para su verificacion algebraica,
cambia mi querida catrina,
archus=√(〖claps〗^2 )+〖bithais〗^2
bithais=√(〖claps〗^2 )+〖archus〗^2
claps=√(〖archus〗^2 )+〖bithais〗^2
Hemos terminado,dijo Pitágoras,
la catrina muy contenta,
se puso a bailar,
al fin había entendido sin tanto practicar.
Se fueron a comer
al puesto de Don José,
agarrados de la mano,
esperando que yo saque 10.
domingo, 16 de octubre de 2016
TRIÁNGULO
A) MEDIANA:
La mediana de un triangulo es el segmento que une uno de sus vértices con el centro del costado opuesto. Hay tres medianas (ma, mb y mc), según de que vértice para esta. Las tres medianas de un triangulo confluyen en un punto llamado baricentro o centroide (G). En cualquier mediana, la distancia entre el baricentro o centroide y el centro de su lado correspondientes es 1/3 de la longitud de dicha mediana.
B)MEDIATRIZ:
La mediatriz de un segmento es la recta perpendicular a dicho segmento trazada por su punto medio. Equivalentemente se puede definir como el lugar geométrico de todos los puntos que son equidistantes a los extremos del segmento.Las mediatrices de los lados de un triángulo se cortan en un punto común, el cual es el centro de la única circunferencia a la que pertenecen los tres vértices del triángulo. Este punto se denomina Circuncentro.
C) ALTURA DE UN TRIÁNGULO
La altura de un objeto o figura geométrica es una longitud o una distancia de una dimensión geométrica, usualmente vertical o en la dirección de la gravedad.
D)BISECTRIZ:
Recta que al pasar por un ángulo lo divide en dos partes iguales geométricamente, los puntos de la bisectriz son paralelos, es decir, tienen la misma distancia en las semirrectas de un ángulo.
E) BARICENTRO:
El baricentro es el punto de corte de las tres medianas; las medianas de un triángulo son las rectas que unen el punto medio de un lado del triángulo con el vértice opuesto. El baricentro se expresa con la letra G.
F) INCENTRO:
Es el punto de corte de las tres bisetrices. Es el centro de una circunferencia inscrita en el triángulo.
G) ORTOCENTRO:
Punto de intersección en el cual confluyen las tres altitudes de un triangulo. Es decir, en el ortocentro se cortan las tres alturas de un triangulo.
H) RECTA DE EULER:
En todo triángulo no equilátero, se cumple la siguiente propiedad: el otrocentro (H), el baricentro (G) y el circuncentro (O) están alineados. La recta que contiene estos tres puntos se llama recta de Euler.
TRIÁNGULO
Es un polígono de tres segmentos que determinan tres puntos del plano y su limitación. Cada punto dado pertenece a dos segmentos. Los puntos comunes a cada par de segmentos se denominan vértices del triángulo y los segmentos de recta determinados son los lados del triángulo. Dos lados contiguos forman uno de los ángulos interiores del triángulo. Un triángulo es una figura estrictamente convexa.Un triángulo tiene tres ángulos interiores, tres pares congruentes de ángulos exteriores, tres lados y tres vértices entre otros elementos.
COORDENADAS
A(-14,-4) B(-8,8) C(12,-2)
PENDIENTES
m=(Y2-Y1)/(X2-X1)
mAB=(8+4)/(-8+14)=12/6=4/2
mBC=(8+2)/(-8-12)=10/(-20)=5/(-10)
mAC=(-2+4)/(12+14)=2/26=1/13
PUNTO MEDIO
X= X1+X2
2
Y=Y1+Y2
2
PMAB=-14-8=-22= -11 4+8=4=2
2 2 2 2
PMAB= (-11,2)
PMCA= 12-14=-2=-1 -2-4=-6=-3
2 2 2 2
PMCA= 8-1,-3)
PMBC=-8+12=4=2 8-2=6=3
2 2 2 2
PMBC=(2,3)
MEDIANAS:
A(-14,-4), PMBC (2,39
Punto,punto
Y-YI=Y2-Y1=(X-X1)
X2-X1
Y+4=3+4=(X+14)
2+14
Y+4=7(X+14)
16
16y+64=7x+98
SI: 7x-16y+34=0
B(-8,8) PMCA (-1,-3)
Punto,punto
Y-8=3-8=(X+8)
-1+8
Y-8=-11(X+8)
7
7y-8=-11x+8
S2: 11x+7y-16=0
C(12,-2) PMAB= (-11,2)
Punto,punto
Y+2=2+2=(X+12)
-11-12
Y+2=4(X+12)
-23
-23y+2=4x+12
S3: 4x+23y-14=0
BARICENTRO
EC1= 11x+7y-16=0
EC2= 4x+23y-14=0
253x+161y-368
-28x-161y+98
225x-270=0
x=-270
225
x=1.2
Sustitución
4(1.2)+23y-14=0
4.8+23y-14=0
23y=-4.8+14
23y=9.2
y=9.2
23
y=0.4
martes, 20 de septiembre de 2016
MAPAS DE LOCALIZACIÓN
A) INTRODUCCIÓN TEÓRICO: CARTOGRÁFICA E IMPORTANCIA DE LOS MAPAS.
https://www.google.com.mx/maps/dir/CCH+Oriente,+Avenida+Canal+de+San+Juan,+Agr%C3%ADcola+Oriental/Iztacala+Fes,+CUSI+Iztacala,+Enrique+Villase%C3%B1or,+Habit.+Los+Reyes+Ixtacala+Barrio+de+los+%C3%81rboles%2FBarrio+de+los+H%C3%A9roes,+M%C3%A9x./@19.4476433,-99.1737808,12z/data=!4m14!4m13!1m5!1m1!1s0x85d1fda96926368d:0xf0be84163012a174!2m2!1d-99.0608776!2d19.3828444!1m5!1m1!1s0x85d1f7ff05a1e6e3:0xaa45f3ab13086aac!2m2!1d-99.1866342!2d19.5273113!3e3?hl=es-419
Automóvil:
https://www.google.com.mx/maps/dir/CCH+Oriente,+Avenida+Canal+de+San+Juan,+Agr%C3%ADcola+Oriental/Colegio+De+Ciencias+Y+Humanidades+Plantel+Azcapotzalco,+Av.+Aquiles+Serdan+2060,+Azcapotzalco,+Ex-hacienda+del+Rosario,+02020+Ciudad+de+M%C3%A9xico,+D.F./@19.4437672,-99.1668868,13z/am=t/data=!4m15!4m14!1m5!1m1!1s0x85d1fda96926368d:0xf0be84163012a174!2m2!1d-99.0608776!2d19.3828444!1m5!1m1!1s0x85d20297d30ca9c3:0x86dacdcac8c255bd!2m2!1d-99.2043854!2d19.4995693!3e3!5i2?hl=es-419
Los mapas son una
representación terrestre a escala en un plano, estos son importantes ya que no
solo representan las tierras, sino también los ríos, lagos, zonas montañosas,
entre otros, lo cual es indispensable para que a la hora de conocer un país, estado
o lugar podamos saber cuáles son las zonas que lo conforman. Hoy en día se ha
vuelto vital el uso de los mapas ya que los medios de transporte necesitan
tener un conocimiento exacto de los diversos lugares que hay en el planeta,
para así poder realizar sus movimientos; no solo hablamos de los medios de transporte
para viajes a larga distancia, sino también del que utilizamos diariamente para
trasladarnos de un lugar a otro, puesto que los conductores necesitan saber
rutas alternativas para cuando haya mucho tráfico o cualquier otra
circunstancia que les impida el paso.
Los mapas se utilizan como modelos para representar
las diversas características del planeta Tierra, hay distintos tipos de mapas (climáticos,
demográficos, geológicos, etc.) que nos ayudan a realizar con seguridad
diversas actividades como son: la extracción de los minerales, la agricultura,
la intensidad de la lluvia, la radiación solar y el estudio de la población. Esta
representación incluye una serie de elementos cartográficos, como son la
escala, la orientación, la localización, la distribución y los símbolos, que
pueden ser puntos, líneas. Todo esto está presente día a día en nuestra vida
diaria, y en cuanto a lo educativo hace que nosotros podamos adaptarnos a
nuestro medio, saber que nos afecta, pero sobre todo desarrollar aptitudes para
poder conocer más del mundo en que vivimos.
B) MAPA DE LOCALIZACIÓN
ORIGEN: CCH ORIENTE
DESTINO: FES IZTACALA
Transporte Público
https://www.google.com.mx/maps/dir/CCH+Oriente,+Avenida+Canal+de+San+Juan,+Agr%C3%ADcola+Oriental/Iztacala+Fes,+CUSI+Iztacala,+Enrique+Villase%C3%B1or,+Habit.+Los+Reyes+Ixtacala+Barrio+de+los+%C3%81rboles%2FBarrio+de+los+H%C3%A9roes,+M%C3%A9x./@19.4476433,-99.1737808,12z/data=!4m14!4m13!1m5!1m1!1s0x85d1fda96926368d:0xf0be84163012a174!2m2!1d-99.0608776!2d19.3828444!1m5!1m1!1s0x85d1f7ff05a1e6e3:0xaa45f3ab13086aac!2m2!1d-99.1866342!2d19.5273113!3e3?hl=es-419
Automóvil:
ORIGEN: CCH ORIENTE
DESTINO: CCH AZCAPOTZALCO
Transporte Público
AUTOMÓVIL
UNIDADES DE MEDIDA DE UN ÁNGULO
A)
MARCO TEÓRICO:
CONCEPTO DE ANGULO
Se conoce
como ángulo a la porción del plano comprendida entre dos
semirrectas con un origen común llamado vértice. Se hace referencia a
un punto en común, con dos líneas que parten desde ese punto y que generan
una cierta apertura, representada por un arco. El concepto de ángulo,
entonces, hace referencia a una magnitud que puede ser analizada y comparada con
otras, por lo que existen operaciones entre ellos.
FORMA DE MEDIR UN ÁNGULO
-Medición en grados
Un ángulo formado por la
rotación completa tiene una medida de 360 grados (3600). Un ángulo formado por
1/360 de una rotación completa tiene una medida de 1 grado (10). El símbolo “0”
denota grados.
-Medición en radianes
Si el vértice de un ángulo 
se coloca en el centro de un circulo con radio 
, y la longitud del arco que subtiende sobre la circunferencia es S, entonces la medida en radianes de 
esta dada por:
se coloca en el centro de un circulo con radio , y la longitud del arco que subtiende sobre la circunferencia es S, entonces la medida en radianes de esta dada por:
radianes.
s: longitud del arco
r: radio circunferencia
ÁNGULOS POSITIVOS
Los ángulos positivos sobre el circulo unidad se miden con la parte inicial en lo positivo X-eje y el lado del terminal se mueve en sentido contrario a las manecillas del reloj.
ÁNGULOS NEGATIVOS
Si se mide en el sentido de giro de las agujas del reloj, se considera negativo. Cualquier ángulo se puede medir en sentido positivo o en sentido negativo. La suma de los valores absolutos de las dos medidas es igual a 360°.
UNIDADES DE MEDIDA (SISTEMA)
RADIANES
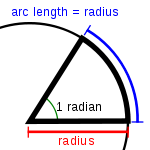
Un radian es la unidad de medida de un ángulo con vértice en el centro de un círculo cuyos lados son cortados por el arco de la circunferencia, y que además dicho arco tiene una longitud igual a la del radio.
El ángulo formado por dos radios de una circunferencia, medido en radianes, es igual a la longitud del arco que delimitan los radios dividida entre el radio; es decir, θ = s/r, donde θ es el ángulo, s es la longitud de arco, y r es el radio. Por tanto, el ángulo completo, , que subtiende una circunferencia de radio r, medido en radianes, es:
, que subtiende una 
El radián es la unidad de ángulo plano en el Sistema Internacional de Unidades. Representa el ángulo central en una circunferencia y abarca un arco cuya longitud es igual a la del radio.
GRADOS
Es la unidad empleada para clasificar los ángulos en las figuras geométricas (generalmente entre dos rectas o segmentos). Existen no obstante varias escalas:
- Grado centesimal, cuando la circunferencia se divide en 400 grados.
La unidad de medida de ángulos del sistema sexagesimal es el grado (°), que es el resultado de dividir el ángulo llano en 180 partes iguales. Así, un ángulo recto mide 90°. Cada grado se divide en 60 minutos (´ )y, cada minuto, en 60 segundos ( ´´ ).
- B) INTRODUCCIÓN TEÓRICA
- Se realizo un proyecto en el cuál se tenia que demostrar como se obtiene el valor de pi (3.1416) en una circunferencia. En este caso el procedimiento fue así:
- Se tenía que calcular el diámetro (12 cm) y después dividirlo entre dos, realizando esta operación se obtiene el radio (6 cm). Después con un material como estambre, hilo, listón, cinta adhesiva (en este caso se utilizó diurex de diferentes colores) se tenían que cortar 6 pedazos iguales del tamaño del radio y pegarlos alrededor de la circunferencia, por ultimo el espacio que sobraba era el valor de pi. Recordando que una revolución es igual a 360° y esto equivale a 2pi radianes.
Suscribirse a:
Entradas (Atom)